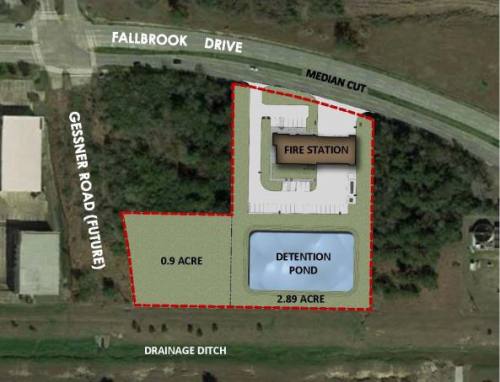
Harris County ESD No. 13 and the Cypress Creek Fire Department finalized a deal in late August to purchase about four acres of land where officials plan to build the department's fifth fire station.
The deal, announced in a September press release, is for a tract of land near the intersection of Gessner Road and Fallbrook Drive, inside the northwest corner of Beltway 8. The final sale price was not disclosed.
The land purchase comes roughly four months after
voters approved a ballot measure allowing the district to collect a portion of sales tax revenue on goods sold within its boundaries. The measure—approved by 65.7% of voters—increased the sales tax in the area from 7.25% to 8.25%, with the additional percentage point going to the Fire Department. That bump is expected to translate into around $1.1 million in additional revenue per year.
At the time, district officials
made the case that the new station was needed to serve a growing but difficult to reach area around Gessner and Fallbrook. Without the bump in sales tax revenue to help fund the new station, the department would have likely had to relocate another one of its stations closer to the area in question, Fire Chief Richard Lieder said.
In the September press release, Lieder said the new station will help firefighters provide better response times.
"With the implementation of the fifth fire station, we will better serve the residents within our district," he said. "Since Harvey, we have identified a plan to do more for our constituents, and this station will provide better response times with fully trained staff."
The station, which is being built by Joiner Architects, is expected to be complete by mid-2021. Department officials said they plan to purchase a new fire engine for the station, which will be staffed 24/7. CCFD is also looking into a partnership with Cypress Creek Emergency Medical Services to bring a full-time, staffed medic unit to the station, according to the release.
CCFD serves an estimated 80,000 residents. A map of the district's boundaries can be found
here.